7. Mechanics of fluids

 

 

 

We now apply the general principles described in the preceding chapters to specific problems.  In this chapter, we give a short introduction to the governing equations for fluids, and give solutions to some simple boundary value problems.

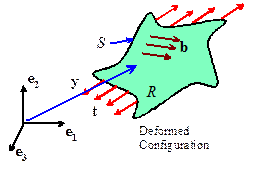
7.1 Summary of governing equations for fluids

 

Fluids have (by definition) the following properties:

(1)   A fluid has no natural reference configuration, so all governing equations are expressed in spatial form.  The lack of reference configuration also means that the response of the fluid can only depend on kinematic variables that characterize motion only of the current configuration $–$ i.e. the velocity gradient, and measures derived from it.

(2)   A fluid at rest can support no shear stress $–$ the stress state in a stationary fluid is just a hydrostatic pressure, which may vary with position.

 

The central problem in a fluid mechanics problem is generally to determine the velocity distribution $v(y,t)$, Cauchy stress distribution ${\sigma }_{ij}$ and (sometimes) temperature $\theta$, as functions of position and time.  The fluid is characterized by the following physical quantities:

 The mass density $\rho$

 The specific internal energy $\epsilon$

 The specific entropy $s$

 The specific Helmholtz free energy $\psi =\epsilon -\theta s$

 A stress response function ${\sigma }_{ij}={\widehat{\sigma }}_{ij}(\theta ,\rho ,\text{kinematic and internal variables)}$

 A heat flux response function $q_i={\widehat{q}}_i(\theta ,\rho ,\text{kinematic and internal variables)}$

 

Body forces: The fluid is subjected to an external body force $b_i$ per unit mass.

 

Its motion is characterized by the usual deformation measures

  Velocity Gradient $L_{ij}=\frac{\partial v_i}{\partial y_j}$

  Strain rate decomposition $L_{ij}=D_{ij}+W_{ij}{D}_{ij}=(L_{ij}+L_{ji})/2W_{ij}=(L_{ij}-L_{ji})/2$

  Vorticity ${\omega }_i={\in }_{ijk}\frac{\partial v_k}{\partial y_j}$

  Vorticity-Spin relation $\omega =2dual(W){\omega }_i=-{\in }_{ijk}{W}_{jk}$

 Velocity-acceleration relations

 

$\begin{array}{l}{a}_i={\frac{\partial v_i}{\partial t}|}_{x_k=const}=\frac{\partial v_i}{\partial y_k}\frac{\partial y_k}{\partial t}+{\frac{\partial v_i}{\partial t}|}_{y_i=const}=L_{ik}{v}_k+{\frac{\partial v_i}{\partial t}|}_{y_i=const}=\left(D_{ik}+W_{ik}\right)v_k+{\frac{\partial v_i}{\partial t}|}_{y_i=const}\\ =\frac{1}{2}\frac{\partial }{\partial y_i}(v_k{v}_k)+2W_{ik}{v}_k={\frac{\partial v_i}{\partial t}|}_{y_k=const}+\frac{1}{2}\frac{\partial }{\partial y_i}(v_k{v}_k)+{\in }_{ijk}{\omega }_j{v}_k\\ {\in }_{ijk}\frac{\partial a_k}{\partial y_j}={\frac{\partial {\omega }_i}{\partial t}|}_{x=const}-D_{ij}{\omega }_j+\frac{\partial v_k}{\partial y_k}{\omega }_i\end{array}$

 

 

and is governed by the standard Conservation laws:

 

  Mass Conservation ${\frac{\partial \rho }{\partial t}|}_{x=const}+\rho D_{kk}=0\text{or }{\frac{\partial \rho }{\partial t}|}_{y=const}+\frac{\partial \rho v_i}{\partial y_i}=0$

  Linear momentum conservation $\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i=\rho \left(\frac{\partial v_i}{\partial y_k}{v}_k+{\frac{\partial v_i}{\partial t}|}_{y_i=const}\right)$

  Energy conservation $\rho {\frac{\partial \epsilon }{\partial t}|}_{x=const}={\sigma }_{ij}{D}_{ij}-\frac{\partial q_i}{\partial y_i}+q$

 

Finally the constitutive law must satisfy the Entropy Inequality: ${\sigma }_{ij}{D}_{ij}-\frac{1}{\theta }{q}_i\frac{\partial \theta }{\partial y_i}-\rho \left(\frac{\partial \psi }{\partial t}+s\frac{\partial \theta }{\partial t}\right)\ge 0$

 

Transformations under observer changes:

  Velocity Gradient $L^{*}=QL{Q}^T+\dot{Q}{Q}^T$

  Stretch rate $D^{*}=QL{Q}^T$

  Spin $W^{*}=QW{Q}^T+\dot{Q}{Q}^T$

  Cauchy Stress ${\sigma }^{*}=Q\sigma Q^T$

 

 

7.2 General Form for Constitutive equations for fluids: 

 

We now list the general form of the constitutive equations for a fluid that are consistent with frame indifference and the entropy inequality.  In practice, most problems of interest are approximated using one of several special cases of the general equations.  These will be listed separately.

 

To be consistent with frame indifference and the laws of thermodynamics, the specific free energy, internal energy, Helmholtz free energy, stress response function and heat transfer function must have the forms

 Specific internal energy $\epsilon =\widehat{\epsilon }(\rho ,\theta )$

 Specific entropy $s=\widehat{s}(\rho ,\theta )$

 Specific Helmholtz free energy $\psi =\widehat{\psi }(\rho ,\theta )=\epsilon -\theta s$

 Stress response function ${\sigma }_{ij}={\widehat{\sigma }}_{ij}(\theta ,\rho ,D_{ij})=-{\widehat{\pi }}_{eq}(\rho ,\theta ){\delta }_{ij}+{\widehat{\sigma }}_{ij}^{vis}(\rho ,\theta ,D_{ij})$ 

    with ${\widehat{\sigma }}_{ij}^{vis}(\rho ,\theta ,0)=0$.  Here, ${\pi }_{eq}$ can be interpreted as the pressure that would be measured in the fluid with density $\rho$ and temperature $\theta$ when at rest.   This decomposition is given a-priori, and is constructed to ensure that the stress state in a fluid at rest supports zero shear stress.

 Heat flux response function $q_i={\widehat{q}}_i\left(\theta ,\rho ,\frac{\partial \theta }{\partial y_i},D_{ij}\right)$

It is useful also to introduce the specific heat at constant volume $c_v(\theta ,\rho )=\frac{\partial \widehat{\epsilon }}{\partial \theta }$

 

Then, the equilibrium pressure ${\widehat{\pi }}_{eq}$, free energy, entropy and specific heat capacity are related by

$\begin{array}{l}{\widehat{\pi }}_{eq}={\rho }^2\frac{\partial \widehat{\psi }}{\partial \rho }\widehat{s}=-\frac{\partial \psi }{\partial \theta }\\ \frac{\partial {\widehat{\pi }}_{eq}}{\partial \theta }=-{\rho }^2\frac{\partial \widehat{s}}{\partial \rho }{\widehat{\pi }}_{eq}=\theta \frac{\partial {\widehat{\pi }}_{eq}}{\partial \theta }+{\rho }^2\frac{\partial \widehat{\epsilon }}{\partial \rho }\\ c_v=-\theta \frac{{\partial }^2\widehat{\psi }}{\partial {\theta }^2}\frac{\partial c_v}{\partial \rho }=-\frac{\theta }{{\rho }^2}\frac{{\partial }^2{\widehat{\pi }}_{eq}}{\partial {\theta }^2}\end{array}$

In addition, the viscous stress and heat flux functions must satisfy

${\sigma }_{ij}^{vis}(\rho ,\theta ,D_{ij})D_{ij}\ge 0q_i\left(\rho ,\theta ,\frac{\partial \theta }{\partial y_i}\right)\frac{\partial \theta }{\partial y_i}\ge 0$

 

We next summarize the reasoning that leads to these conclusions:

 

·         Frame indifference shows that the free energy function and the stress and heat transfer response functions depend only on the symmetric part of the velocity gradient (i.e. the stretch rate), and must be isotropic functions.  To see this, note that frame indifference requires that

$\begin{array}{l}\widehat{\psi }(\rho ,\theta ,L)=\widehat{\psi }(\rho ,\theta ,QL{Q}^T+\dot{Q}{Q}^T)\\ Q_{ik}{\widehat{\sigma }}_{kl}(\rho ,\theta ,L)Q_{jl}={\widehat{\sigma }}_{ij}(\rho ,\theta ,QL{Q}^T+\dot{Q}{Q}^T)\\ Q_{ik}{\widehat{q}}_k\left(\theta ,\rho ,\nabla \theta ,L\right)={\widehat{q}}_i\left(\theta ,\rho ,Q\nabla \theta ,QL{Q}^T+\dot{Q}{Q}^T\right)\end{array}$

for all proper orthogonal tensors $Q(t)$.  Recall that $L=D+W$.  If we choose $\dot{Q}=\Omega Q$ with $\Omega$ an arbitrary skew tensor such that $Q(0)=I$, then $\dot{Q}{Q}^T=\Omega$, and applying frame indifference at time t=0 then gives

$\begin{array}{l}\widehat{\psi }(\rho ,\theta ,L)=\widehat{\psi }(\rho ,\theta ,D+W+\Omega )\\ {\widehat{\sigma }}_{ij}(\rho ,\theta ,L)={\widehat{\sigma }}_{ij}(\rho ,\theta ,D+W+\Omega )\\ {\widehat{q}}_i\left(\theta ,\rho ,\nabla \theta ,L\right)={\widehat{q}}_i\left(\theta ,\rho ,\nabla \theta ,D+W+\Omega \right)\end{array}$

Then, selecting $W=-\Omega$ shows that $\widehat{\psi }(\rho ,\theta ,L)=\widehat{\psi }(\rho ,\theta ,D){\widehat{\sigma }}_{ij}(\rho ,\theta ,L)={\widehat{\sigma }}_{ij}(\rho ,\theta ,D)$.  Finally, with arbitrary Q, we see that

$\begin{array}{l}\widehat{\psi }(\rho ,\theta ,D)=\widehat{\psi }(\rho ,\theta ,QD{Q}^T)\\ Q_{ik}{\widehat{\sigma }}_{kl}(\rho ,\theta ,D)Q_{jl}={\widehat{\sigma }}_{ij}(\rho ,\theta ,QD{Q}^T)\\ Q_{ik}{\widehat{q}}_k\left(\theta ,\rho ,\nabla \theta ,D\right)={\widehat{q}}_i\left(\theta ,\rho ,Q\nabla \theta ,QD{Q}^T\right)\end{array}$

This implies that the free energy and stress and heat transfer response functions are all isotropic functions.

 

Not everyone agrees with the argument that constitutive behavior must be independent of spin.  This conclusion relies on the assumption that the response functions are invariant to changes between reference frames that are rotating relative to one another.   If invariance is required only to transformations between frames that have a fixed relative velocity and orientation, spin can enter in the constitutive behavior.   Some models of turbulent flow do include spin.

 

·         The free energy inequality provides the remaining conclusions.   Take the time derivative of the free energy function and substitute into the free energy inequality to see that

${\sigma }_{ij}{D}_{ij}-\frac{1}{\theta }{q}_i\frac{\partial \theta }{\partial y_i}-\rho \left(\frac{\partial \psi }{\partial \rho }\dot{\rho }+\frac{\partial \psi }{\partial \theta }\dot{\theta }+\frac{\partial \psi }{\partial D_{ij}}{\dot{D}}_{ij}+s\frac{\partial \theta }{\partial t}\right)\ge 0$

(time derivatives are all with fixed x). Note that

${\sigma }_{ij}{D}_{ij}=-{\widehat{\pi }}_{eq}(\rho ,\theta )D_{ii}+{\widehat{\sigma }}_{ij}^{vis}(\rho ,\theta ,D_{ij})D_{ij}$

and also recall that from mass conservation $\dot{\rho }+\rho D_{kk}=0$.  Collecting coefficients of rate quantities we see that

$\left({\rho }^2\frac{\partial \psi }{\partial \rho }-{\widehat{\pi }}_{eq}(\rho ,\theta )\right)D_{ii}+{\widehat{\sigma }}_{ij}^{vis}(\rho ,\theta ,D_{ij})D_{ij}-\frac{\partial \psi }{\partial D_{ij}}{\dot{D}}_{ij}-\frac{1}{\theta }{q}_i\frac{\partial \theta }{\partial y_i}-\rho \left(\frac{\partial \psi }{\partial \theta }+s\right)\frac{\partial \theta }{\partial t}\ge 0$

This inequality must hold for all possible $D_{ij},{\dot{D}}_{ij},\dot{\theta },\partial \theta /\partial y_i$, which can all be independently prescribed.   It follows immediately that

$\frac{\partial \psi }{\partial D_{ij}}=0s=-\frac{\partial \psi }{\partial \theta }\frac{1}{\theta }{q}_i\frac{\partial \theta }{\partial y_i}\le 0$

Next, note that

$\left({\rho }^2\frac{\partial \psi }{\partial \rho }-{\widehat{\pi }}_{eq}(\rho ,\theta )\right)D_{ii}+{\widehat{\sigma }}_{ij}^{vis}(\rho ,\theta ,D_{ij})D_{ij}\ge 0$

and replace $D_{ij}$ with $\alpha D_{ij}$ with $\alpha >0$ it follows that

$\left({\rho }^2\frac{\partial \psi }{\partial \rho }-{\widehat{\pi }}_{eq}(\rho ,\theta )\right)D_{ii}+{\widehat{\sigma }}_{ij}^{vis}(\rho ,\theta ,\alpha D_{ij})D_{ij}\ge 0$

We can now let $\alpha \to 0$ and since ${\widehat{\sigma }}_{ij}^{vis}(\rho ,\theta ,0)=0$ we see that

${\widehat{\pi }}_{eq}(\rho ,\theta )={\rho }^2\frac{\partial \psi }{\partial \rho }{\widehat{\sigma }}_{ij}^{vis}(\rho ,\theta ,D_{ij})D_{ij}\ge 0$

 

·         The remaining identities follow from these results, together with the definition $\psi =\epsilon -\theta s$ .  This implies that

$\begin{array}{l}\frac{d\psi }{dt}=\frac{\partial \psi }{\partial \rho }\dot{\rho }+\frac{\partial \psi }{\partial \theta }\dot{\theta }=-{\pi }_{eq}\frac{\dot{\rho }}{{\rho }^2}-s\dot{\theta }\\ \frac{d\psi }{dt}=\frac{d\epsilon }{dt}-\frac{d\theta }{dt}s-\theta \frac{ds}{dt}\Rightarrow \frac{d\epsilon }{dt}=-{\pi }_{eq}\frac{\dot{\rho }}{{\rho }^2}+\theta \dot{s}\end{array}$

In addition, since

${\pi }_{eq}={\rho }^2\frac{\partial \psi }{\partial \rho }s=-\frac{\partial \psi }{\partial \theta }\Rightarrow {\rho }^2\frac{{\partial }^2\psi }{\partial \rho \partial \theta }=\frac{\partial {\pi }_{eq}}{\partial \theta }=-{\rho }^2\frac{\partial s}{\partial \rho }$

whence

$\frac{\partial \psi }{\partial \rho }=\frac{\partial \epsilon }{\partial \rho }-\theta \frac{\partial s}{\partial \rho }\Rightarrow \frac{{\pi }_{eq}}{{\rho }^2}=\frac{\partial \epsilon }{\partial \rho }+\frac{\theta }{{\rho }^2}\frac{\partial {\pi }_{eq}}{\partial \theta }$

The definitions of free energy and heat capacity also show that

$\frac{\partial \psi }{\partial \theta }=\frac{\partial \epsilon }{\partial \theta }-s-\theta \frac{\partial s}{\partial \theta }\Rightarrow \frac{\partial \epsilon }{\partial \theta }=c=\theta \frac{\partial s}{\partial \theta }=-\theta \frac{{\partial }^2\psi }{\partial {\theta }^2}$

Furthermore

$\frac{\partial c}{\partial \rho }=-\theta \frac{{\partial }^2}{\partial {\theta }^2}\frac{\partial \psi }{\partial \rho }=-\frac{\theta }{{\rho }^2}\frac{{\partial }^2{\pi }_{eq}}{\partial {\theta }^2}$

 

 

7.3 Special cases of constitutive equations for fluids

 

The following special cases of constitutive equations are frequently used in fluid mechanics:

 

 An Elastic fluid (also known as a barotropic fluid or Eulerian fluid) has free energy and stress response independent of temperature

$\psi =\widehat{\psi }(\rho ){\sigma }_{ij}=-{\pi }_{eq}(\rho ){\delta }_{ij}$

Its heat capacity is zero, and heat flow is not usually considered in applications that use this model. Either the free energy, or the pressure, must be fit to experiment.   The two are related through the equations listed in the preceding section.

 

 An Ideal Gas has free energy and stress response function

$\epsilon =c_v\theta =\frac{p}{(\gamma -1)\rho }\psi =c_v\theta -\theta \left(c_v\log \theta -R\log \rho -s_0\right){\sigma }_{ij}=-p{\delta }_{ij}=-\rho R\theta {\delta }_{ij}$

where R is the gas constant, $c_v$ is the specific heat capacity (a constant), and $s_0$ is an arbitrary constant.  Ideal gases are also characterized by the specific heat at constant pressure $c_p=c_v+R$ and the ratio $\gamma =c_p/c_v$.  An ideal gas is inviscid.  Pressure, temperature and density in an ideal gas are related by the equation of state $p=\rho R\theta$.  Note that R in these equations is the individual gas constant, which has units of Joules/kg/Kelvin, and varies from one gas to another.   It can be computed from the universal gas constant $R_u=8.314J/mol/K$ using the relation $R=R_u/m$ where m is the molecular weight of the gas (the mass of one mole of the gas).

 

 A Compressible Linear (Newtonian) Viscous Fluid has free energy and stress response function

$\psi =\widehat{\psi }(\rho ,\theta ){\sigma }_{ij}=-({\pi }_{eq}(\rho ,\theta )-\kappa (\rho ,\theta )D_{kk}){\delta }_{ij}+2\eta (\rho ,\theta )(D_{ij}-D_{kk}{\delta }_{ij}/3)$

where $\kappa ,\eta$ are functions of density and temperature that must be fit to experiment.  They are known as the bulk and shear viscosity of a fluid, respectively.

 

 A Compressible nonlinear (non-Newtonian) Viscous Fluid has free energy and stress response function

$\begin{array}{l}\psi =\widehat{\psi }(\rho ,\theta )\\ {\sigma }_{ij}=-{\pi }_{eq}(\rho ,\theta ){\delta }_{ij}+{\eta }_1(I_1,I_2,I_3,\rho ,\theta ){\delta }_{ij}+{\eta }_2(I_1,I_2,I_3,\rho ,\theta )D_{ij}+{\eta }_3(I_1,I_2,I_3,\rho ,\theta )D_{ik}{D}_{kj}\end{array}$

where $I_1,I_2,I_3$ are the three invariants of $D_{ij}$, and  ${\eta }_1,{\eta }_2,{\eta }_3$ are three functions that must be fit to experiment.

 

 

Heat Flux: For all these cases, in problems where heat flow is considered, it is most common to set

$q_i=-k(\rho ,\theta )\frac{\partial \theta }{\partial y_i}$

where k is the thermal conductivity (often taken to be constant).

 

 

 

7.4 Special forms of field equations for viscous fluids

 

The flow of a viscous fluid is governed by

(i)                 The mass balance equation

(ii)               The linear momentum balance equation

(iii)             The constitutive law for a compressible, or incompressible viscous fluid

(iv)             In problems with heat transfer, the energy conservation equation.

together with any relevant boundary conditions.  For calculations, it is convenient to combine (ii) and (iii) to obtain a single equation relating the static pressure and velocity, with the following results

 

 The Compressible Navier-Stokes Equation is a convenient form of the linear momentum balance equations for a compressible, linear viscous fluid.

$-\frac{\partial p}{\partial y_i}+2\frac{\partial }{\partial y_j}\eta (\rho ,\theta )\left(D_{ij}-D_{kk}{\delta }_{ij}/3\right)+\rho b_i=\rho {\frac{d{v}_i}{dt}|}_{x=const}p={\pi }_{eq}(\rho ,\theta )-\kappa (\rho ,\theta )D_{kk}$

 

 For the case of Density independent viscosity this equation can be simplified to

$-\frac{1}{\rho }\frac{\partial {\pi }_{eq}}{\partial y_i}+\frac{\eta }{\rho }\frac{{\partial }^2{v}_i}{\partial y_j\partial y_j}+\left(\frac{\kappa }{\rho }-\frac{2\eta }{3\rho }\right)\frac{{\partial }^2{v}_j}{\partial y_j\partial y_i}+b_i={\frac{d{v}_i}{dt}|}_{x=const}={\frac{\partial v_i}{\partial t}|}_{y_k=const}+\frac{1}{2}\frac{\partial }{\partial y_i}(v_k{v}_k)+{\in }_{ijk}{\omega }_j{v}_k$

 

 The Vorticity transport equation governs evolution of vorticity in a fluid with density independent viscosity at constant temperature.  It has the form 

$+\frac{\eta }{\rho }\frac{{\partial }^2{\omega }_i}{\partial y_j\partial y_j}-\frac{1}{{\rho }^2}{\in }_{ijk}\frac{\partial \rho }{\partial y_j}\left\{\eta \frac{{\partial }^2{v}_k}{\partial y_l\partial y_l}+\left(\kappa -\frac{2\eta }{3}\right)\frac{{\partial }^2{v}_l}{\partial y_l\partial y_k}\right\}+{\in }_{ijk}\frac{\partial }{\partial x_j}(b_k)+D_{ij}{\omega }_j-\frac{\partial v_k}{\partial y_k}{\omega }_i={\frac{\partial {\omega }_i}{\partial t}|}_{x=const}$

This result is not especially useful for viscous, compressible flows, but simplifies considerably if the fluid is incompressible, or if the viscosity can be neglected.   The result can be derived as follows:  

(i)                 Recall first that ${\pi }_{eq}={\rho }^2\frac{\partial \psi }{\partial \rho }$.  It follows (by direct substitution, noting that temperature is constant) that

$\frac{1}{\rho }\frac{\partial {\pi }_{eq}}{\partial y_i}=\frac{\partial }{\partial y_i}\left(\psi +\frac{{\pi }_{eq}}{\rho }\right)$

 

(ii)               The Navier-Stokes equation can therefore be rearranged as

$-\frac{\partial }{\partial y_i}\left(\psi +\frac{{\pi }_{eq}}{\rho }\right)+\frac{\eta }{\rho }\frac{{\partial }^2{v}_i}{\partial y_j\partial y_j}+\left(\kappa -\frac{2\eta }{3}\right)\frac{1}{\rho }\frac{{\partial }^2{v}_j}{\partial y_j\partial y_i}+b_i={\frac{d{v}_i}{dt}|}_{x=const}$

(iii)             Taking the curl of both sides, recalling curl(grad(f))=0, and expressing the curl of the acceleration in terms of vorticity we then obtain

$+\frac{\eta }{\rho }\frac{{\partial }^2{\omega }_i}{\partial y_j\partial y_j}-\frac{1}{{\rho }^2}{\in }_{ijk}\frac{\partial \rho }{\partial y_j}\left\{\eta \frac{{\partial }^2{v}_k}{\partial y_l\partial y_l}+\left(\kappa -\frac{2\eta }{3}\right)\frac{{\partial }^2{v}_l}{\partial y_l\partial y_k}\right\}+{\in }_{ijk}\frac{\partial }{\partial y_j}(b_k)={\frac{\partial {\omega }_i}{\partial t}|}_{x=const}-D_{ij}{\omega }_j+\frac{\partial v_k}{\partial y_k}{\omega }_i$

 

 

 The Entropy Equation is a useful result for analyzing gas flows.   It states that the rate of change of specific entropy at a point in a compressible viscous fluid can be computed from

${\rho \theta \frac{\partial s}{dt}|}_{x=const}=\kappa (\rho ,\theta )D_{kk}{D}_{jj}+2\eta (D_{ij}{D}_{ij}-D_{kk}{D}_{jj}/3)-\frac{\partial q_i}{\partial y_i}+q$

 

To see this, start with the identity $\psi =\epsilon -\theta s$.   It follows that

$\dot{\psi }=\frac{\partial \psi }{\partial \rho }\dot{\rho }+\frac{\partial \psi }{\partial \theta }\dot{\theta }=\dot{\epsilon }-\theta \dot{s}-s\dot{\theta }\Rightarrow \theta \dot{s}=\dot{\epsilon }-\frac{{\pi }_{eq}}{{\rho }^2}\dot{\rho }$

Next, recall the mass conservation and energy conservation equations

${\frac{\partial \rho }{\partial t}|}_{x=const}+\rho D_{kk}=0\rho {\frac{\partial \epsilon }{\partial t}|}_{x=const}={\sigma }_{ij}{D}_{ij}-\frac{\partial q_i}{\partial y_i}+q$

The constitutive equations also show that

${\sigma }_{ij}{D}_{ij}=-({\pi }_{eq}-\kappa D_{kk})D_{jj}+2\eta (D_{ij}{D}_{ij}-D_{kk}{D}_{jj}/3)$

Thus

$\theta \dot{s}=\kappa D_{kk}{D}_{jj}+2\eta (D_{ij}{D}_{ij}-D_{kk}{D}_{jj}/3)-\frac{\partial q_i}{\partial y_i}+q$

 

 

7.5 Special forms of field equations for elastic fluids

 

For elastic fluids, we can show the following results

 

 Euler’s equations of motion are the special cases of the linear momentum balance equation for elastic fluids

$-\frac{\partial {\pi }_{eq}}{\partial y_i}+\rho b_i=\rho {\frac{\partial v_i}{\partial t}|}_{y_k=const}+\frac{1}{2}\rho \frac{\partial }{\partial y_i}(v_k{v}_k)+\rho {\in }_{ijk}{\omega }_j{v}_k$

(the acceleration can be written in many other forms, of course)

 

 The Vorticity transport equation for an elastic fluid reduces to 

${\in }_{ijk}\frac{\partial }{\partial x_j}(b_k)+D_{ij}{\omega }_j-\frac{\partial v_k}{\partial y_k}{\omega }_i={\frac{\partial {\omega }_i}{\partial t}|}_{x=const}$

An important conclusion from this result is that if the body force can be derived from a potential (so its curl vanishes), and the flow is irrotational at time t=0, it remains irrotational.

 

 Bernoulli’s equation is a special result governing steady flow of an elastic fluid that is subjected to conservative body forces.  Conservative body forces can be described by a potential energy, so that $b_i=-\partial \Phi /\partial y_i$.  Then, the Bernoulli equation states that, along a streamline

$H=\psi +\frac{{\pi }_{eq}}{\rho }+\frac{1}{2}{v}_i{v}_i+\Phi =\text{constant}$

Recall that a streamline is a curve that is everywhere tangent to the velocity vector (for steady flow, the streamlines are coincident with the trajectories traced by material particles).  For the particular case of irrotational flow, this quantity is constant and independent of position. 

 

This result can be derived as follows.   First, recall that

$\frac{1}{\rho }\frac{\partial {\pi }_{eq}}{\partial y_i}=\frac{\partial }{\partial y_i}\left(\psi +\frac{{\pi }_{eq}}{\rho }\right)$

Noting that steady flow implies that ${\partial v_i/\partial t|}_{y=const}=0$, the momentum balance equation therefore reads

$-\frac{\partial }{\partial y_i}\left(\psi +\frac{{\pi }_{eq}}{\rho }+\Phi \right)=\frac{1}{2}\frac{\partial }{\partial y_i}(v_k{v}_k)+{\in }_{ijk}{\omega }_j{v}_k$

For irrotational flow ${\omega }_j=0$, and this equation can then be integrated to obtain the Bernoulli equation.  Similarly, taking the dot product of both sides of this equation with the velocity vector and rearranging shows that

$-v_i\frac{\partial }{\partial y_i}\left(\psi +\frac{{\pi }_{eq}}{\rho }+\frac{1}{2}{v}_k{v}_k+\Phi \right)=0$

and therefore $\psi +\frac{{\pi }_{eq}}{\rho }+\frac{1}{2}{v}_i{v}_i+\Phi =\text{constant}$ along streamlines. 

 

 

 

 

7.6 Incompressible flow

 

In many cases fluids can be approximated as incompressible, which simplifies the governing equations further.  

 

 The mass balance equation reduces to

$\frac{\partial v_i}{\partial y_i}=0$

 The Incompressible Navier-Stokes Equation can be simplified to

$-\frac{1}{\rho }\frac{\partial p}{\partial y_i}+\frac{\eta }{\rho }\frac{{\partial }^2{v}_i}{\partial y_j\partial v_j}+b_i={\frac{d{v}_i}{dt}|}_{x=const}={\frac{\partial v_i}{\partial t}|}_{y_k=const}+\frac{1}{2}\frac{\partial }{\partial y_i}(v_k{v}_k)+{\in }_{ijk}{\omega }_j{v}_k$

The quantity $\nu =\eta /\rho$ is known as the kinematic viscosity.

 

 The Vorticity transport equation reduces to 

$+\frac{\eta }{\rho }\frac{{\partial }^2{\omega }_i}{\partial y_j\partial y_j}+{\in }_{ijk}\frac{\partial }{\partial x_j}(b_k)+D_{ij}{\omega }_j={\frac{\partial {\omega }_i}{\partial t}|}_{x=const}$

 

 

 

7.7 Incompressible, inviscid, irrotational flow (potential flow)

 

If a flow field is irrotational, the velocity field can be derived from a scalar potential

$v_i=\frac{\partial \varphi }{\partial y_i}$

(it is easy to show that $v_i$ of this form is irrotational.  The converse can be shown for fluids occupying a simply connected region $–$ the potential may be multiple valued for multiply connected regions). 

 

 If a fluid is incompressible its velocity field (assuming irrotational flow) can be computed by solving for $\varphi$.   In particular

  Mass Conservation yields the governing equation for $\varphi$: $\frac{\partial v_i}{\partial y_i}=\frac{{\partial }^2\varphi }{\partial y_i\partial y_i}=0$

 If the fluid is inviscid, then Bernoulli’s equation (generalized to time dependent flow) yields the governing equation for the pressure

$\frac{p}{\rho }+\frac{1}{2}\frac{\partial \varphi }{\partial y_i}\frac{\partial \varphi }{\partial y_i}+\Phi +\frac{\partial \varphi }{\partial t}=f(t)$

where $-\partial \Phi /\partial y_i=b_i$  is the potential for body force per unit mass, and f(t) is an arbitrary function of time.   Since the flow is irrotational, this expression holds everywhere (not just along streamlines).

 

Together with appropriate boundary conditions, these equations determine both the velocity and pressure associated with the flow.

 

 

7.8 Stokes Flow

 

The general Navier-Stokes equation is nonlinear, because of the terms involving the square of the velocity in the acceleration.   If these terms can be neglected (as is the case for flows with low values of Reynolds number $\mathrm{Re}=\rho VL/\eta$, where V and L are a representative velocity and length), the Navier-Stokes equation can be approximated as

$-\frac{1}{\rho }\frac{\partial p}{\partial y_i}+\frac{\eta }{\rho }\frac{{\partial }^2{v}_i}{\partial y_j\partial v_j}+b_i\approx {\frac{\partial v_i}{\partial t}|}_{y_k=const}$

Velocity fields that satisfy this equation are known as Stokes Flows.  For steady flows, or for particularly slow flows, the equation can be simplified further by setting $\partial v_i/\partial t=0$.

 

 

7.9 Boundary conditions for fluid flow problems

 

There are three common types of fluid mechanics problem:

1.     A rigid or elastic solid which moves through a stationary fluid or gas;

2.     A bubble of gas or fluid of a second phase moves through a surrounding fluid;

3.     A fluid or gas flows through rigid or elastic walls of some sort.   

 

The following boundary conditions are most commonly used in these problems:

1. Where a viscous fluid meets a solid boundary, the fluid is usually assumed to have the same velocity as the solid surface (both normal and tangential components of velocity are equal).  This is the no slip boundary condition.  Normal and tangential components of traction must also be continuous across the interface.

 

2. Where an inviscid fluid meets a solid boundary, the normal component of velocity must be equal in both solid and fluid where the two meet.   The tangential component of velocity may be discontinuous.   The normal component of traction is continuous across the boundary, and the shear traction vanishes.

 

 

3. A bubble inside a fluid is usually assumed to be inviscid, and tractions are required to be continuous across the fluid/gas interface.   For small bubbles, it may be necessary to account for the effects of surface tension as well.   In this case, the solid/fluid interface must be modeled as a separate phase, with its own constitutive behavior.  It is above our pay-grade to discuss this in detail here, but the basic concepts we develop here for solid and fluid phases should be sufficient for you to be able to follow texts and papers that work through the thermodynamics of interfaces.

 

4. In some high-speed compressible viscous flow problems; or in microfluidics applications, the no-slip boundary condition is found to be inaccurate.  In this case the tangential component of velocity may be discontinuous across the boundary.  An additional constitutive law must specify a relationship between the tractions acting on the interface and the velocity discontinuity.

 

 

7.10 Control surface method for fluid flow problems

 

The control surface method is a helpful approach to computing average quantities such as resultant forces exerted by a fluid flow on a surface.   

 

The method relies on the conservation laws for a control volume

 

 Mass Conservation: $\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho dV}+{\displaystyle \underset{B}{\int }\rho v\cdot ndA}=0$

 Linear Momentum Balance ${\displaystyle \underset{B}{\int }n\cdot \sigma dA}+{\displaystyle \underset{R}{\int }\rho bdV}=\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho v}dV+{\displaystyle \underset{B}{\int }(\rho v)v\cdot ndA}$

 Angular Momentum Balance ${\displaystyle \underset{B}{\int }y\times (n\cdot \sigma )dA}+{\displaystyle \underset{R}{\int }y\times (\rho b)dA}=\frac{d}{dt}{\displaystyle \underset{R}{\int }y\times \rho vdV}+{\displaystyle \underset{B}{\int }(y\times \rho v)v\cdot ndA}$

 Mechanical Power Balance

${\displaystyle \underset{B}{\int }(n\cdot \sigma )\cdot vdA}+{\displaystyle \underset{R}{\int }\rho b\cdot v}dV={\displaystyle \underset{R}{\int }\sigma :D}dV+\frac{d}{dt}{\displaystyle \underset{R}{\int }\frac{1}{2}\rho (v\cdot v)dV}+{\displaystyle \underset{B}{\int }\frac{1}{2}\rho (v\cdot v)v\cdot ndA}$

 First law of thermodynamics

${\displaystyle \underset{B}{\int }(n\cdot \sigma )\cdot v}dA+{\displaystyle \underset{R}{\int }\rho b\cdot v}dV-{\displaystyle \underset{B}{\int }q\cdot ndA}+{\displaystyle \underset{V}{\int }qdV}=\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho \left(\epsilon +\frac{1}{2}v\cdot v\right)dV}+{\displaystyle \underset{B}{\int }\rho \left(\epsilon +\frac{1}{2}v\cdot v\right)v\cdot n}dA$

 Second law of thermodynamics $\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho sdV}+{\displaystyle \underset{B}{\int }\rho s(v\cdot n)dA}+{\displaystyle \underset{B}{\int }\frac{q\cdot n}{\theta }dA}-{\displaystyle \underset{R}{\int }\frac{q}{\theta }dV}\ge 0$

 

 

 

In addition, the Bernoulli equation can be applied to inviscid, incompressible flows along a streamline .  In this case it has the form

$\frac{p}{\rho }+\frac{1}{2}{v}_i{v}_i+\Phi =\text{constant}$

where $-\partial \Phi /\partial y_i=b_i$ is the body force per unit mass.

 

 

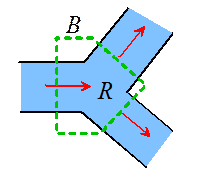
Example 1: A jet of incompressible, inviscid fluid with mass density ${\rho }_0$, cross sectional area $A_0$, and speed $v_0$ is incident on an inclined wall, as shown in the figure. The surrounding atmostpheric pressure is $p_0$ and gravity may be neglected. Calculate the force acting on the wall.

 

 

 

1. Consider a control volume as shown in the figure, with interior R and boundary B.
2. Note that ${\displaystyle \underset{B}{\int }{p}_{0}ndA}=0$
3. Note that the fluid is inviscid, and therefore the shear stress acting on the wall vanishes.  Momentum balance in the j direction thus shows that

${\displaystyle \underset{A}{\int }(-p_{0}n\cdot jdA})j-A_0{\rho }_0{v}_0^2\sin \alpha j+{\displaystyle \underset{A_3}{\int }(p-p_0)dAj}=0$

4. We recognize the last integral as the force exerted by the wall on the fluid.  The force exerted by the fluid on the wall must be equal and opposite, and so $F=-A_0{\rho }_0{v}_0^2\sin \alpha j$

 

 

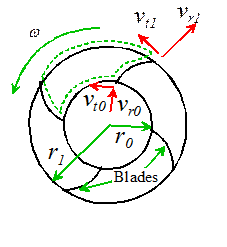
Example 2: The figure shows an idealized centrifugal pump.   Fluid enters the rotating blades with radial and tangential velocity $(v_{r0,}{v}_{t0})$ and exits with velocity $(v_{r1,}{v}_{t1})$.   The tangential velocity of the fluid is equal to that of the blades at both entry and exit.   The blades rotate with angular speed $\omega$ and the mass flow rate through the pump is $\dot{m}$.   Calculate the torque required to rotate the pump.

 

1. Consider a control volume consisting of the annular region occupied by the blades, but excluding the blades themselves (only one piece of the CV is shown in the figure)
2. Assume axisymmetric flow $–$ so fluid velocity is independent of $\theta$
3. Mass conservation gives $2\pi r_{0}z{v}_{r0}\rho =2\pi r_{1}z{v}_{r1}\rho =\dot{m}$, where z is the out of plane depth of the blades.
4. The angular momentum equation gives

${\displaystyle \underset{B}{\int }y\times (n\cdot \sigma )dA}={\displaystyle \underset{B}{\int }(y\times \rho v)v\cdot ndA}$

The integral on the left represents the net moment exerted by the blades on the fluid.  The contributions to the integral on the right from the surfaces adjacent to the blades cancel, leaving only the contributions from the inner and outer surfaces of the annulus.   Evaluating the integrals gives

$M_z=2\pi r_1(z{r}_1{v}_{t1})v_{n1}\rho -2\pi r_0(z{r}_0{v}_{t0})v_{n0}\rho$

5. Note that $v_{t1}=r_1\omega v_{t0}=r_0\omega$, which gives $M_z=\dot{m}\omega (r_1^2-r_0^2)$.

 

 

Example 3: For our third example, we work through Von Karman’s classic estimate of the drag force on a stationary plate inside a steadily flowing stream.   The figure shows the problem to be solved.   Ahead of the plate, the fluid has a uniform horizontal velocity $V$ with direction parallel to the edge of the plate.   A boundary layer in which the fluid flow is slowed develops adjacent to the plate, and as a result the horizontal velocity has profile $v_1(y_2)$ at the trailing edge of the plate.    The velocity field is assumed to be uniform outside the boundary layer. $$ We assume that the width of the boundary layer $\delta$ at the trailing edge of the plate can be determined somehow.   Our goal is then to determine the drag force on the plate in terms of $v_1(y_2)$, L  and the mass density of the fluid $\rho$.  

 

We choose a control volume that is bounded by the plate, and at the top follows a streamline outside the boundary layer which terminates at the trailing edge of the boundary layer.   The pressure outside this control volume is uniform.  No fluid crosses the upper or lower surfaces of the control volume, and we assume steady-state conditions.

 

  Mass conservation then implies that

$\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho dV}+{\displaystyle \underset{B}{\int }\rho v\cdot ndA}=0\Rightarrow -\rho Vh+{\displaystyle \underset{0}{\overset{\delta }{\int }}\rho v_1(y_2)d{y}_2=0}$

 

Linear momentum balance shows that

$\begin{array}{l}{\displaystyle \underset{B}{\int }n\cdot \sigma dA}+{\displaystyle \underset{R}{\int }\rho bdV}=\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho v}dV+{\displaystyle \underset{B}{\int }(\rho v)v\cdot ndA}\\ \Rightarrow {\displaystyle \underset{B}{\int }n\cdot \sigma dA}=-\rho V^{2}h+{\displaystyle \underset{0}{\overset{\delta }{\int }}\rho {\left[v_1(y_2)\right]}^{2}d{y}_2}\end{array}$

Only the plate exerts a force on the control volume (the pressure is uniform, and there is no shear stress acting on the top surface of the control volume because the velocity is uniform), so we recognize the integral on the left as the resultant force exerted by the plate on the control volume.   The drag force exerted by the fluid on the plate must be equal and opposite.

 

Substituting for h from the first equation into the second, and noting that a boundary layer must form on both sides of the plate, gives the following expression for the total drag force

 

$F_D=2{\displaystyle \underset{0}{\overset{\delta }{\int }}\rho v_1(y_2)\left[V-v_1(y_2)\right]d{y}_2}$

The formula is only useful if the velocity profile at the trailing edge of the plate is known.  As a rough guess, we could take a parabolic velocity distribution which satisfies $v=0$ at y=0 and $v=V,dv/dy=0$ at $y=\delta$.   This then yields

$v_1(y_2)=V\left(2\frac{y_2}{\delta }-{\left(\frac{y_2}{\delta }\right)}^2\right)\Rightarrow F_D=\frac{4\rho \delta V^2}{15}$

To use this expression we still need to find the thickness of the boundary layer, but that’s beyond our pay-grade.   An asymptotic analysis gives $\delta =4.65L/(\rho VL/\eta )$, where $\eta$ is the fluid viscosity.

 

 

 

7.11 Exact solutions to simple incompressible, inviscid, irrotational flow problems (potential flow)

 

The governing equations for potential flow can be reduced to:

 The solution can be generated from a harmonic potential satisfying $\frac{{\partial }^2\varphi }{\partial y_i\partial y_i}=0$. 

 The velocity components follow as $v_i=\frac{\partial \varphi }{\partial y_i}$

 The velocity must satisfy $v_i{n}_i=V_i{n}_i$ at any point where it meets a surface with normal $n_i$ moving with velocity $V_i$

 The pressure can be computed from the Bernoulli equation

$\frac{p}{\rho }+\frac{1}{2}\frac{\partial \varphi }{\partial y_i}\frac{\partial \varphi }{\partial y_i}+\Phi +\frac{\partial \varphi }{\partial t}=\frac{p_0}{\rho }$

where $p_0$ is a reference pressure at some point where the velocity and body force potential are zero.

 

It is relatively straightforward to solve the Laplace equation $–$ in 3D, many solutions have been found by guesswork; techniques such as Fourier transforms can be used to solve more complex problems.   In 2D, complex variable methods are very effective.   It turns out that both the real and imaginary parts of a differentiable function of a complex number (eg a polynomial function of a complex number z=x+iy) are solutions to Laplace’s equation.   Techniques such as conformal mapping and analytic continuation are also useful.  We don’t have time in this course to discuss these procedures in detail $–$ instead, we just list a few important solutions.

 

 

 

 

 

 

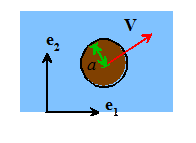7.11.1 Flow surrounding a moving sphere

 

The flow surrounding a rigid sphere with radius a that starts at the origin, and then moves without rotation with velocity $V_i$ can be computed from the following potential

$\varphi =-\frac{a^3{V}_i(y_i-V_{i}t)}{2r^3}r=\sqrt{(y_k-V_{k}t)(y_k-V_{k}t)}$

 

7.11.2 Flow surrounding a moving cylinder

 

The flow surrounding a rigid cylinder that moves without rotation with velocity $V_i$ can be computed from the following potential

$\varphi =-\frac{a^2{V}_{\alpha }(y_{\alpha }-V_{\alpha }t)}{2r^2}r=\sqrt{(y_{\alpha }-V_{\alpha }t)(y_{\alpha }-V_{\alpha }t)}$

 

As an exercise, you might like to calculate (i) The components of the velocity field; (ii) the pressure distribution acting on the sphere and cylinder; (iii) The drag force acting on the sphere and cylinder (the result is surprising at first, but note that there is no dissipation so at steady-state there can be no drag; (iv) the total kinetic energy in the fluid.

 

 

 

7.12 Solutions to simple viscous flow problems (Stokes flow)

 

The equations governing Stokes flow are also fairly easy to solve, because the equations are linear.  This means that Fourier transform techniques and complex variable methods both work.   We won’t try to cover these here, but list a few examples of solutions to Stokes flow problems

 

 

 

7.12.1 Laminar flow of an incompressible viscous fluid between plates

 

The problem to be solved is illustrated in the figure.  An incompressible fluid with mass density $\rho$ and viscosity $\eta$ is confined between parallel plates.  External boundary constraints at the ends of the plate induce a (constant) pressure gradient $\Delta p/\Delta L$ in a direction parallel to the plates.  The top plate moves with speed V, and the bottom is stationary.

 

The velocity field in the fluid has the form

$\begin{array}{l}v=\left[V\frac{y_2}{h}-\frac{\Delta p}{2\Delta L}{y}_2(h-y_2)\right]e_1\\ \sigma =\frac{\eta V}{h}+\frac{\Delta p}{\Delta L}\left(\frac{h}{2}-y_2\right)\end{array}$

These results can be derived as follows. 

1.     Boundary conditions at the top and bottom surfaces of the plate suggest that the flow velocity must be parallel to the plates, and independent of $y_1$.  We can assume that $v=f(y_2)e_1$

2.     The flow is steady, so the general Navier-Stokes equation reduces to

$-\frac{1}{\rho }\frac{\partial p}{\partial y_i}+\frac{\eta }{\rho }\frac{{\partial }^2{v}_i}{\partial y_j\partial v_j}+b_i\approx {\frac{\partial v_i}{\partial t}|}_{y_k=const}\Rightarrow -\frac{\Delta p}{\Delta L}+\eta \frac{{\partial }^{2}f}{\partial y_2^2}=0$

3.     We can easily integrate this equation to see that $f=A{y}_2+B+\frac{\Delta p}{2\Delta L}{y}_2^2$

4.     Boundary conditions at  the plate surfaces imply that $f(0)=0f(h)=V$.  We can then solve for the unknown constants A and B, giving the answer stated.

 

 

7.12.3 Rigid sphere moving at steady speed through a viscous fluid

 

The velocity field surrounding a rigid sphere that moves without rotation with instantaneous velocity $V_i$ through a viscous fluid is

$\begin{array}{l}{v}_i=\frac{3a{V}_j}{4r^5}(r^2-a^2)(y_j-V_{j}t)(y_i-V_{i}t)+\frac{a{V}_i}{4r^3}(3r^2+a^2)\\ r=\sqrt{(y_i-V_{i}t)(y_i-V_{i}t)}\end{array}$

For $r>>a$ the velocity field can be approximated as

$v_i=\frac{3a{V}_j}{4r^3}(y_j-V_{j}t)(y_i-V_{i}t)+\frac{3a{V}_i}{4r}$

This solution is called a ‘Stokeslet.’  The Stokeslet solution can also be expressed in terms of the force exerted by the sphere on the fluid $–$ for a sphere at the origin we have

$v_i=\frac{P_j}{8\eta r}\left(\frac{y_i{y}_j}{r^2}+{\delta }_{ij}\right)$

 

 

7.12.3 Spherical bubble moving at steady speed through a viscous fluid

 

The velocity field surrounding a spherical bubble that moves with instantaneous velocity $V_i$ through a viscous fluid is

$v_i=\frac{a{V}_j}{2r}\left({\delta }_{ij}+\frac{(y_i-V_{i}t)(y_j-V_{j}t)}{r^2}\right)r=\sqrt{(y_i-V_{i}t)(y_i-V_{i}t)}$

 

 

 

7.13 Solutions to simple compressible flow problems

 

Many compressible flow problems are concerned with flows in air, which can often be approximated as an ideal gas.  The governing equations for an ideal gas reduce to

 

 Mass conservation

${\frac{\partial \rho }{\partial t}|}_{x=const}+\rho \frac{\partial v_i}{\partial y_i}=0\text{or }{\frac{\partial \rho }{\partial t}|}_{y=const}+\frac{\partial \rho v_i}{\partial y_i}=0$

  Navier Stokes

$-\frac{\partial p}{\partial y_i}+\rho b_i=\rho {\frac{d{v}_i}{dt}|}_{x=const}=\rho {\frac{\partial v_i}{\partial t}|}_{y_k=const}+\frac{1}{2}\rho \frac{\partial }{\partial y_i}(v_k{v}_k)+\rho {\in }_{ijk}{\omega }_j{v}_k$

 Energy conservation

$\rho {\frac{\partial \epsilon }{\partial t}|}_{x=const}=-p\frac{\partial v_i}{\partial y_i}-\frac{\partial q_i}{\partial y_i}+q$

 Entropy equation

$\theta {\frac{\partial s}{\partial t}|}_{x=const}=-\frac{\partial q_i}{\partial y_i}+q$

 Constitutive law: internal energy, free energy and stress response function

$\epsilon =c_v\theta \psi =c_v\theta -\theta \left(c_v\log \theta -R\log \rho +s_0\right)p=\rho R\theta$

where R is the gas constant, $c_v$ is the specific heat capacity (a constant), and $s_0$ is an arbitrary constant.  Ideal gases are also characterized by the specific heat at constant pressure $c_p=c_v+R$ and the ratio $\gamma =c_p/c_v$.

 

 

7.13.1 Sound waves in an ideal gas

 

Small amplitude sound waves can be approximated as a small variation in density and pressure superimposed on a static state.    The velocity field for a small amplitude acoustic wave in still air is irrotational, and the velocity field and the change in density in the gas satisfy the equations

$\frac{{\partial }^2{v}_i}{\partial t^2}-c_s^2\frac{{\partial }^2{v}_j}{\partial y_i\partial y_j}=0\frac{{\partial }^2\delta \rho }{\partial t^2}-c_s^2\frac{\partial \delta \rho }{\partial y_i\partial y_i}=0$

where

$c_s=\sqrt{{\frac{\partial p}{\partial \rho }|}_{s=const}}$

is the speed of sound. In actual calculations it is often convenient to introduce a flow potential $\varphi$ that satisfies

$v_i=\frac{\partial \varphi }{\partial y_i}$

The flow potential satisfies the wave equation

 $\frac{{\partial }^2\varphi }{\partial t^2}-c_s^2\frac{{\partial }^2\varphi }{\partial y_i\partial y_i}=0$

 

These results are derived as follows. 

• It is usually assumed that heat flow can be neglected on the time-scales associated with acoustic vibrations.   This means that the entropy of the gas is constant (see the entropy equation).
• For small perturbations, the change in pressure of the gas is linearly related to its density.  We can write

$\delta p={\frac{\partial p}{\partial \rho }|}_{s=const}\delta \rho$

 

For an ideal gas, it is possible to find a formula for the sound speed. Recall that

$s=-\frac{\partial \psi }{\partial \theta }\Rightarrow s=s_0+\log ({\theta }^{c_v}{\rho }^{-R})\Rightarrow \theta ={\rho }^{R/c_v}\exp ((s+s_0)/c_v)$

and hence, since s=const , $R/c_v=\gamma -1$ and $p=\rho R\theta$ the pressure is related to density by $p=k{\rho }^{\gamma }$ where k is a constant.  It follows that

$c_s=\sqrt{k\gamma {\rho }^{\gamma -1}}=\sqrt{\gamma \frac{p}{\rho }}=\sqrt{\gamma R\theta }$.

·         For small amplitude perturbations, we approximate the Navier-Stokes equation as

$-\frac{\partial p}{\partial y_i}+\rho b_i\approx \rho {\frac{\partial v_i}{\partial t}|}_{y_k=const}$

Taking the time derivative of this expression, and assuming body forces to be independent of time then gives

$-\frac{{\partial }^{2}p}{\partial y_i\partial t}\approx \rho {\frac{{\partial }^2{v}_i}{\partial t^2}|}_{y_k=const}$

·         Note that

$\frac{\partial p}{\partial t}=c_s^2\frac{\partial \delta \rho }{\partial t}$

and linearizing the mass conservation equation shows that

${\frac{\partial \delta \rho }{\partial t}|}_{x=const}+\rho \frac{\partial v_i}{\partial y_i}=0$

Combining these results gives the wave equations.

·         If the fluid is at rest at time t=0 its vorticity vanishes.   The vorticity transport equation then shows that the vorticity must vanish at all times, i.e. the flow is irrotational.   The velocity field therefore satisfies $curl(v)=0$ and hence we can set $v_i=\partial \varphi /\partial y_i$.

 

 

The wave equations can be solved easily for an infinite region.   Two solutions are:

 

Plane waves.  A plane wave can be visualized as a propagating ‘wall’ of sound.  Let $v_i=n_{i}f(y_k{n}_k-c_{s}t)$, where $n_i$ is a unit vector, and f  is an arbitrary function.   This corresponds to a plane wave travelling in a direction parallel to the unit vector $n_i$.  It is easy to show that this velocity field satisfies the wave equation for any f(x).   The density change follows as $\delta \rho =(\rho /c_s)f(y_k{n}_k-c_{s}t)$, and of course the pressure is proportional to the density change.

 

Monopole.    A monopole is a point source of sound.   It would be produced, e.g. by a vanishingly small radially vibrating sphere.  The velocity field has the form

$v_i=\frac{x_i}{4\pi r^2}f(r-c_{s}t)r=\sqrt{x_k{x}_k}$

where f(x) is again an arbitrary function. 

 

 

Dipole.  A dipole is two nearby monopoles emitting equal and opposite signals $–$ it would represent, eg, the sound produced by a sphere moving backwards and forwards along a line.   A loudspeaker that is removed from its box behaves somewhat like a dipole.    The displacement field has the form

$v_i=\frac{(r^2{\delta }_{ij}-x_i{x}_j)n_j}{4\pi r^4}f(r-c_{s}t)r=\sqrt{x_k{x}_k}$

where $n_j$ is a unit vector parallel to the direction of the dipole (eg the direction of the line along which the sphere moves).

 

7.13.2 Flow behind an accelerating piston

 

This is a classic problem that is often used to illustrate the method of characteristics.   The figure shows a piston in a tube that is filled with an ideal gas with mass density ${\rho }_0$ and wave speed $c_0$ (it is more convenient to specify the wave speed than the pressure, but of course the two are related).   At time t=0 the gas and piston are at rest.   The piston then starts to move to the left with constant acceleration a.

 

The velocity field in the gas for $2c_0/a(\gamma -1)>t>0$ is given by

$v=\{\begin{array}{c}-\frac{1}{\gamma }\left[\frac{at(\gamma +1)}{2}+\sqrt{{\left(\frac{at(\gamma +1)}{2}\right)}^2+2ya\gamma }\right]y<c_{0}t\\ 0y\ge c_{0}t\end{array}$

The wave speed can be calculated from the condition

$c=c_0+\left(\gamma -1\right)v/2$

 

These results can be derived as follows. For one-dimensional flow in the y direction, the Navier-Stokes and mass conservation equations reduce to

${\frac{\partial v}{\partial t}|}_{y=const}+v\frac{\partial v}{\partial y}+\frac{c_s^2}{\rho }\frac{\partial \rho }{\partial y}=0{\frac{\partial \rho }{\partial t}|}_{y=const}+v\frac{\partial \rho }{\partial y}+\rho \frac{\partial v}{\partial y}=0$

where $c_s=\sqrt{k{\rho }^{\gamma -1}}$ is the sound speed.  Solving this equation is a bit above our pay-grade in this course, but you are probably covering this material in math, so we’ll work through it anyway. The first step is to write the equations in matrix form

$\frac{\partial q_i}{\partial t}+A_{ij}\frac{\partial q_j}{\partial y}=0q=\left[\begin{array}{c}v\\ \rho \end{array}\right]A=\left[\begin{array}{cc}v& c_s^2/\rho \\ \rho & v\end{array}\right]$

Now, let $\lambda ,r_i$ be a left eigenvalue/eigenvector pair of A.  The eigenvalues/vectors are easily shown to be $(v+c_s),[\rho ,c_s];(v-c_s),[\rho ,-c_s]$. It follows that

$r_i\left(\frac{\partial q_i}{\partial t}+\lambda \frac{\partial q_j}{\partial y}\right)=0$

If we set $\lambda =\partial y/\partial t$ we see further that

$r_i\frac{\partial q_i}{\partial t}=0$

along characteristic lines such that $\partial y/\partial t=v\pm c_s$.  Substituting for $r_i$, $q_i$, we see that

$\rho \frac{\partial v}{\partial t}\pm c_s\frac{\partial \rho }{\partial t}=0\Rightarrow v\pm {\displaystyle \int \frac{c_s}{\rho }d\rho =\text{constant}\Rightarrow v\pm \frac{2}{\gamma -1}{c}_s}=\text{constant}$

These conditions hold along lines satisfying $\partial y/\partial t=v\pm c_s$

 

We can now apply this result to the piston problem. 

·         The (t,y) characteristic diagram is shown in the figure.  The red characteristic lines have slope $\partial y/\partial t=v-c$; the green ones have slope  $\partial y/\partial t=v+c$ (we drop the subscript s for clarity)

·         Note that the red lines terminate in a region where the gas is stationary, and the wave speed is $c_0$.  Therefore $v-2c/(\gamma -1)=-2c_0/(\gamma -1)$ along these lines.  It follows that the wave speed in the moving region of the gas is related to its velocity by $c=c_0+(\gamma -1)v/2$

·         For the green lines, we know $v+2c/(\gamma -1)=B$, with B some constant.   Since each green lines intersects a red one, we already know the wave speed in terms of v, and substituting for c shows that $2v+2c_0/(\gamma -1)=B$.   It follows that v must be constant on the green lines, and therefore they have constant slope $\partial y/\partial t=v+c=v(\gamma +1)/2+c_0$.  We can apply this at the point where the green line intersects the piston (the gas velocity there is equal to that of the piston) to conclude that $\partial y/\partial t=-a{t}_0(\gamma +1)/2+c_0$

·         Integrating, we get $y=-a{t}_0(\gamma +1)t/2+c_{0}t+D$ where D is a  constant of integration $–$ and since we know $y=-a{t}_0^2/2$ at time $t=t_0$ we can solve for D and find that $y=a\gamma t_0^2/2-a{t}_0(\gamma +1)t/2$

·         Finally, we can use this result to solve for the value of $t_0$ corresponding to a general point y at time t in the tube.  The solution is

$t_0=\frac{1}{a\gamma }\left[\frac{at(\gamma +1)}{2}+\sqrt{{\left(\frac{at(\gamma +1)}{2}\right)}^2+2ya\gamma }\right]$

Finally, the velocity at time t of the point y in the tube follows as $v=-a{t}_0$ giving the solution stated.

·         The wave speed follows from $c=c_0+(\gamma -1)v/2$.   Note that at time $t=2c_0/a(\gamma -1)$ the wave speed drops to zero at the piston.  The wave speed can’t be negative, so after this time the piston separates from the gas and a vacuum develops between the piston and the advancing gas.  After this time the gas/vacuum interface moves with speed $-2c_0/(\gamma -1)$.

 

 

7.13.3 Stationary Normal Shock in an ideal gas

 

Shock waves are surfaces in a compressible fluid or gas across which fluid properties and state experience a sharp discontinuity.   They occur between regions where flow is supersonic and subsonic.   The discontinuities across a shock are not arbitrary $–$ they are related by the usual conservation laws and constitutive equations for a fluid.  

 

Consider a stationary shock that separates regions 1 and 2 of a flow.  For simplicity, assume that fluid flows in a direction perpendicular to the plane of the shock. Let $(v_1,p_1,q_1,{\rho }_1,{\epsilon }_1,s_1)$, $(v_2,p_2,q_2,{\rho }_2,{\epsilon }_2,s_2)$ denote the (uniform) velocity, pressure, heat flux, density , specific internal energy and specific entropy just adjacent to the two sides of the shock.

 

Conservation and thermodynamic laws relating these quantities have the following form:

 

 Mass Balance ${\rho }_1{v}_1={\rho }_2{v}_2$

 Linear Momentum Balance $p_1+{\rho }_1{v}_1^2=p_2+{\rho }_2{v}_2^2$

 Energy Conservation (1^st law)  $p_1{v}_1+{\rho }_1{v}_1\left({\epsilon }_1+\frac{1}{2}{v}_1^2\right)+q_1=p_2{v}_2+{\rho }_2{v}_2\left({\epsilon }_2+\frac{1}{2}{v}_2^2\right)+q_2$. 

 Entropy Inequality (2^nd  law)  $\left({\rho }_2{s}_2{v}_2+\frac{q_2}{{\theta }_1}\right)-\left({\rho }_1{s}_1{v}_1+\frac{q_1}{{\theta }_1}\right)\ge 0$

 

 

For an ideal gas, with negligible heat flow, these can be combined to yield several additional relations across a normal shock.

 

 Rankine Hugoniot Relations

${\epsilon }_1-{\epsilon }_2=\frac{1}{2}\left(\frac{1}{{\rho }_2}-\frac{1}{{\rho }_1}\right)(p_1+p_2)\Rightarrow {\lambda }^2\left(\frac{p_1}{{\rho }_1}-\frac{p_2}{{\rho }_2}\right)-\frac{p_1}{{\rho }_2}+\frac{p_2}{{\rho }_1}=0{\lambda }^2=\frac{\gamma -1}{\gamma +1}$

 

 Prandtl’s Relation

$\begin{array}{l}{v}_1{v}_2=c_{*}^2\\ c_{*}^2=(1-{\lambda }^2)c_1^2+{\lambda }^2{v}_1^2=(1-{\lambda }^2)c_2^2+{\lambda }^2{u}_2^2\end{array}$

Prandtl’s relation implies that flow must be supersonic on one side of the shock and subsonic on the other. In addition, to satisfy the entropy inequality, the supersonic flow must be upstream of the shock.

 

 

These results can be derived as follows:  Begin by recalling the conservation laws for a control volume

Mass Conservation: $\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho dV}+{\displaystyle \underset{B}{\int }\rho v\cdot ndA}=0$

Linear Momentum Balance ${\displaystyle \underset{B}{\int }n\cdot \sigma dA}+{\displaystyle \underset{R}{\int }\rho bdV}=\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho v}dV+{\displaystyle \underset{B}{\int }(\rho v)v\cdot ndA}$

First law of thermodynamics

${\displaystyle \underset{B}{\int }(n\cdot \sigma )\cdot v}dA+{\displaystyle \underset{R}{\int }b\cdot v}dV-{\displaystyle \underset{B}{\int }q\cdot ndA}+{\displaystyle \underset{V}{\int }qdV}=\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho \left(\epsilon +\frac{1}{2}v\cdot v\right)dV}+{\displaystyle \underset{B}{\int }\rho \left(\epsilon +\frac{1}{2}v\cdot v\right)v\cdot n}dA$

 

Second law of thermodynamics

$\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho sdV}+{\displaystyle \underset{B}{\int }\rho s(v\cdot n)dA}+{\displaystyle \underset{B}{\int }\frac{q\cdot n}{\theta }dA}-{\displaystyle \underset{R}{\int }\frac{q}{\theta }dV}\ge 0$

Then, introduce a control volume consisting of a narrow rectangular region enclosing the shock.   The thickness can be reduced to zero, so the volume integrals can be made arbitrarily small.  In addition, recall that the stress in an ideal gas is hydrostatic.  Finally, evaluating the separate integrals over the two external surfaces of the control volume and localizing the integrals leads to the conservation relations.

 

The Rankine-Hugoniot relations can be derived from the energy conservation equation

$p_1{v}_1+{\rho }_1{v}_1\left({\epsilon }_1+\frac{1}{2}{v}_1^2\right)=p_2{v}_2+{\rho }_2{v}_2\left({\epsilon }_2+\frac{1}{2}{v}_2^2\right)$

Recall that ${\rho }_1{v}_1={\rho }_2{v}_2$, so this equation can be rearranged as

${\epsilon }_2-{\epsilon }_1=\frac{p_1}{{\rho }_1}-\frac{p_2}{{\rho }_2}+\frac{1}{2}{v}_1^2-\frac{1}{2}{v}_2^2=\frac{p_1}{{\rho }_1}-\frac{p_2}{{\rho }_2}+\frac{1}{2}{\rho }_1^2{v}_1^2\left(\frac{1}{{\rho }_1^2}-\frac{1}{{\rho }_2^2}\right)$

The momentum conservation equation and mass conservation can also be combined to see that

${\rho }_1^2{v}_1^2\left(\frac{1}{{\rho }_1}-\frac{1}{{\rho }_2}\right)=p_2-p_1$

and hence eliminating the velocity term from the energy equation

${\epsilon }_2-{\epsilon }_1=\frac{p_1}{{\rho }_1}-\frac{p_2}{{\rho }_2}+\frac{1}{2}(p_2-p_1)\left(\frac{1}{{\rho }_1}+\frac{1}{{\rho }_2}\right)$

which can be rearranged to give the Rankine Hugoniot relation.   The second identity follows by substituting $\epsilon =\frac{p}{(\gamma -1)\rho }$ for an ideal gas.

 

To show Prandtl’s relation recall that

$c^2=\gamma \frac{p}{\rho }\Rightarrow \epsilon +\frac{p}{\rho }=\frac{1-{\lambda }^2}{2{\lambda }^2}{c}^2$

where ${\lambda }^2=\frac{\gamma -1}{\gamma +1}$.   The energy equation can then be re-written as

${\epsilon }_2+\frac{p_2}{{\rho }_2}+\frac{1}{2}{v}_2^2={\epsilon }_1+\frac{p_1}{{\rho }_1}-+\frac{1}{2}{v}_1^2\Rightarrow \frac{1-{\lambda }^2}{2{\lambda }^2}{c}_2^2+\frac{1}{2}{v}_2^2=\frac{1-{\lambda }^2}{2{\lambda }^2}{c}_1^2+\frac{1}{2}{v}_1^2=\frac{c_{*}^2}{2{\lambda }^2}$

Which then gives the first relation.   To show the second note that

$c^2=\frac{(1+{\lambda }^2)}{(1-{\lambda }^2)}\frac{p}{\rho }$

We can then use the first Prandtl relation to see that

$\begin{array}{l}(1+{\lambda }^2)p_2+{\lambda }^2{\rho }_2{v}_2^2={\rho }_2{c}_{*}^2\\ (1+{\lambda }^2)p_1+{\lambda }^2{\rho }_1{v}_1^2={\rho }_1{c}_{*}^2\\ \Rightarrow (1+{\lambda }^2)(p_2-p_1)+{\lambda }^2{\rho }_1{v}_1{\rho }_2{v}_2\left(\frac{1}{{\rho }_2}-\frac{1}{{\rho }_1}\right)=c_{*}^2({\rho }_2-{\rho }_1)\end{array}$

where we have used mass conservation ${\rho }_1{v}_1={\rho }_2{v}_2$.  Finally, recall that

${\rho }_1{v}_1{\rho }_2{v}_2\left(\frac{1}{{\rho }_1}-\frac{1}{{\rho }_2}\right)=p_2-p_1$

Substituting this into the preceding result and simplifying gives the second Prandtl formula.